“트리는 그래프의 일종이다” 라는 사실을 알게되서 그럼 “그래프 구조” 란 뭘까? 하고 살짝 찾아본다는 게…. 해외 문서까지 찾아가서 정리해버리게 되었네요….
당장은 트리 구조에서 문제를 풀고 있지만 언젠가 다른 그래프 구조의 문제도 해결할 일이 생길 것 같아 기왕 트리를 정리하는 김에 그래프를 몽땅 정리해봤습니다.
GeeksForGeeks라는 사이트에 graph가 너무 자세히 설명되어서 한 번 쭉 읽고 정리해보았습니다.
“그래프” 란?
그래프는 컴퓨터 과학에서 개체 간의 관계를 나타내는 데 사용되는 기본 데이터 구조입니다.
그래프의 개념이 처음에는 추상적으로 들릴 수도 있지만, 일단 분석해 보면 실제로는 매우 간단합니다.
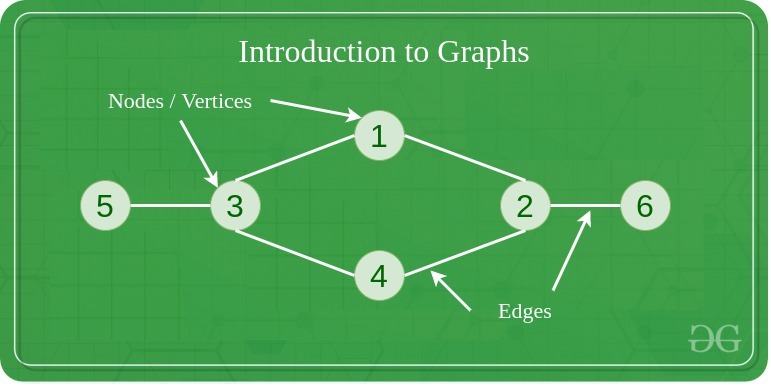
만일 친구 그룹이 있고 누가 누구와 친구인지 표현하고 싶다고 상상해 봅시다.
각 사람을 나타내는 원(node or vertices)과 친구를 연결하는 간선(edges)으로 다이어그램을 그릴 수 있습니다.
이런 다이어그램이 바로 그래프입니다.
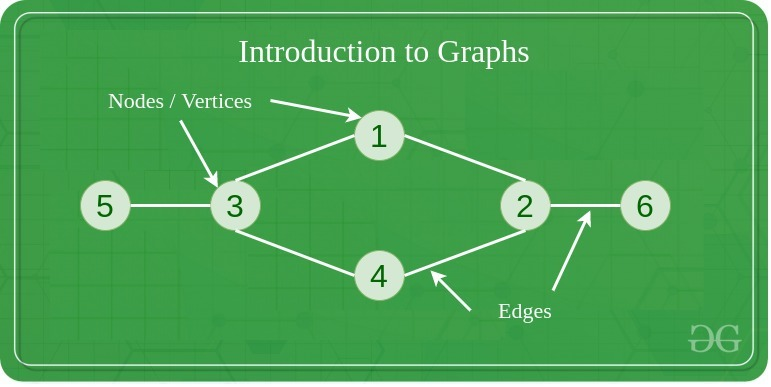
그래프 구조 유형
그래프에는 다양한 유형이 있으며 각각 고유한 특징이 있습니다.
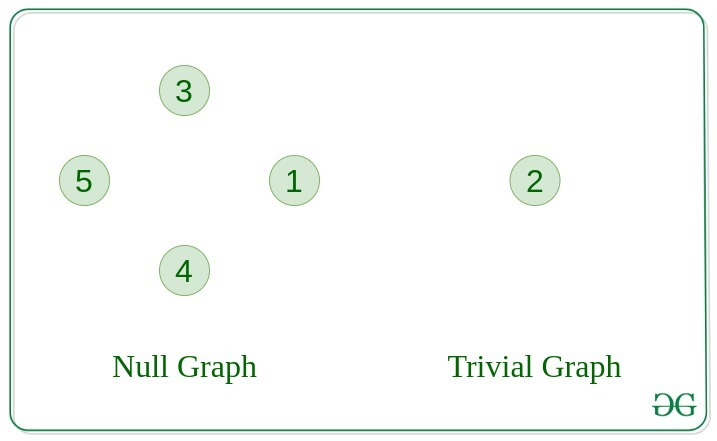
Null 그래프
그래프에 간선이 없으면 그래프를 널 그래프라고 합니다.
Trivial 그래프
노드가 하나만 있는 그래프로, 가능한 가장 작은 그래프이기도 합니다.
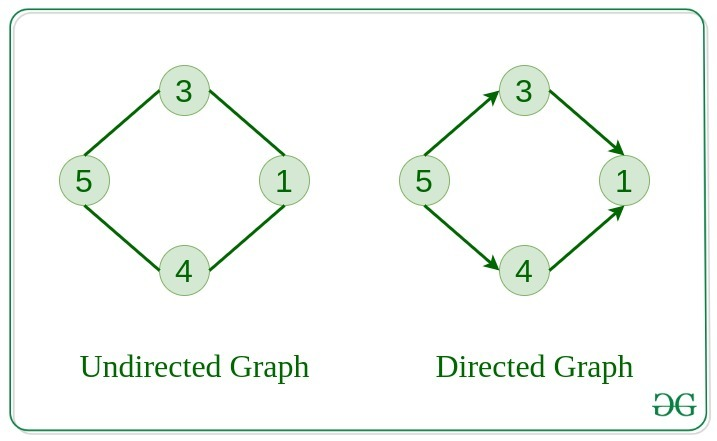
Undirected 그래프
Undirected 그래프에서는 간선에 방향이 없습니다.
노드 A가 노드 B에 연결되면 노드 B도 노드 A에 연결됩니다. 이는 양방향 도로와 같습니다.
Directed 그래프 (Digraphs)
Digraphs에서 edge에는 방향이 있습니다.
노드 A가 노드 B에 연결되어 있다고 해서 반드시 노드 B가 노드 A에 연결되어 있다는 의미는 아닙니다.
일방통행 도로와 같아서 한 방향으로만 이동할 수 있습니다.
Weigthed 그래프
가중치 그래프에서 각 간선에는 이와 관련된 가중치 또는 비용이 있습니다.
이 가중치는 거리, 시간 또는 기타 측정값을 나타낼 수 있습니다.
가중치 그래프는 관계의 강도가 중요한 응용 프로그램에서 일반적으로 사용됩니다.
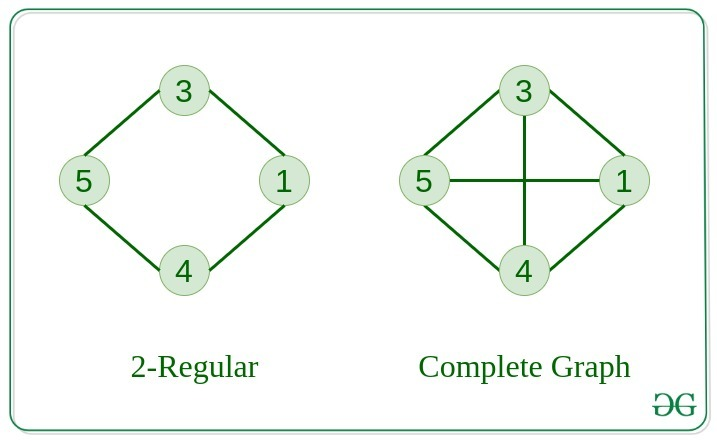
Regular 그래프
정규 그래프(Regular Graph)는 각 노드에 연결된 edge의 수가 동일한 그래프 유형입니다.
모든 사람이 다른 친구와 동일한 수의 연결을 갖고 있는 친구 그룹이라고 생각하시면 될 것 같습니다.
Complete 그래프
complete 그래프는 모든 개별 노드 쌍이 고유한 간선으로 연결된 그래프 유형입니다.
간단히 말해서 모든 사람이 다른 사람과 직접 연결되는 네트워크와 같습니다.
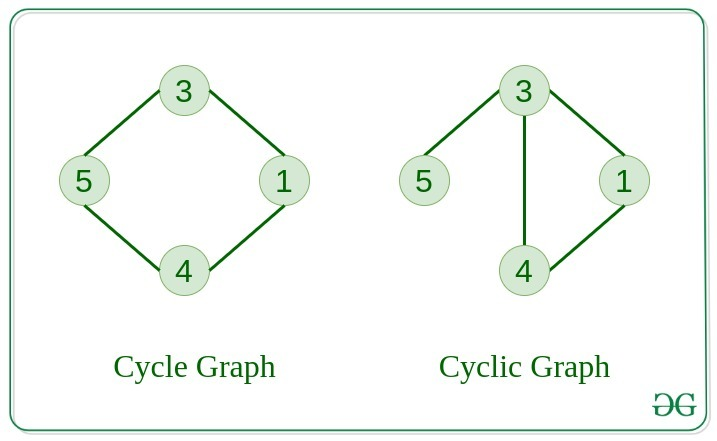
Cycle 그래프
Cycle Graph는 가장자리로 연결된 노드의 단일 폐쇄 루프로 구성된 간단한 유형의 그래프입니다.
Cycle Graph는 정확히 하나의 cycle을 갖는 것이 특징입니다
Cyclic 그래프
순환 그래프(Cyclic Graph)는 간선을 따라가고 다른 경로를 탐색하여 동일한 노드로 돌아갈 수 있는 그래프 유형입니다.
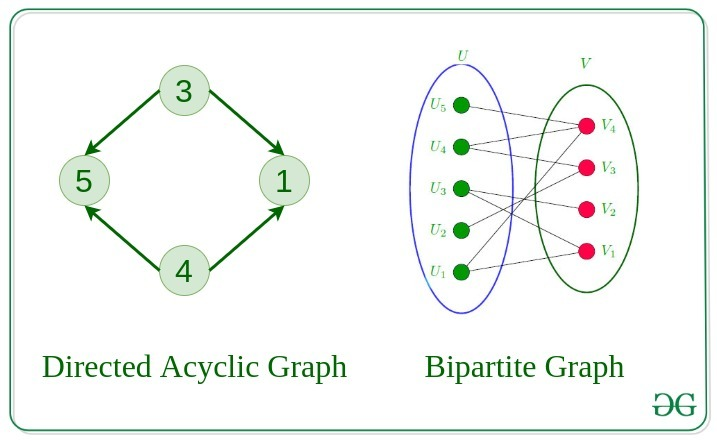
Directed Acyclic 그래프
Directed Acyclic Graph(DAG)는 간선이 특정 방향을 가지며 순환이나 루프가 없는 그래프 유형입니다.
한 단계에서 다음 단계를 가리키는 화살표가 있지만 이전 단계로 돌아가는 루프가 없는 순서도 인거죠.
DAG는 일반적으로 이벤트의 종속성 또는 시퀀스를 나타내는 데 사용되어 프로세스가 반복되지 않고 특정 방향으로 흐르도록 보장합니다.
Bipartite 그래프
이분 그래프(Bipartite Graph)는 노드를 두 개의 개별 그룹으로 나눌 수 있고 모든 간선이 한 그룹의 노드를 다른 그룹에 연결하는 그래프 유형입니다.
손님이 두 팀으로 나뉘어 각 사람이 다른 팀의 구성원하고만 상호 작용할 수 있는 파티라고 생각할 수 있습니다.
이분 그래프는 일반적으로 학생과 수업, 사용자와 관심 분야 등 다양한 유형의 엔터티 간의 관계를 모델링하는 데 사용되며 각 엔터티가 다른 유형의 엔터티와 상호 작용하도록 보장합니다.
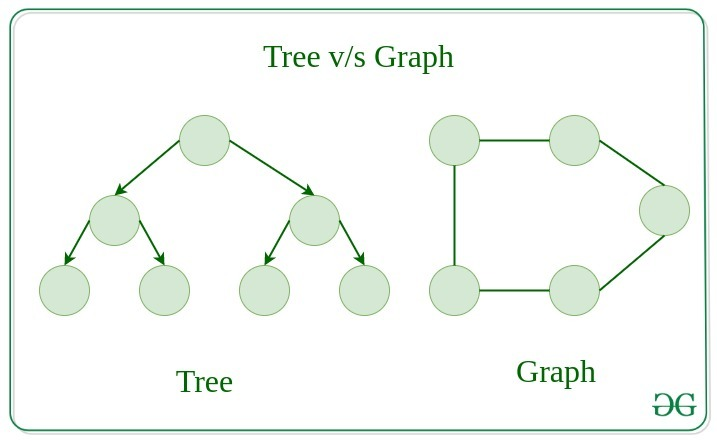
트리 vs 그래프
트리는 각 노드가 루트 노드를 제외하고 정확히 하나의 상위 노드를 가지며 계층 구조를 형성하는 특정 유형의 그래프입니다.
트리는 일반적으로 데이터 구조 및 알고리즘에 사용되어 효율적인 검색 및 순회 작업을 제공합니다.
모든 트리는 그래프이지만 모든 그래프가 트리는 아닙니다.
그래프 구조 표현하기
그래프는 2가지 방법으로 저장될 수 있습니다.
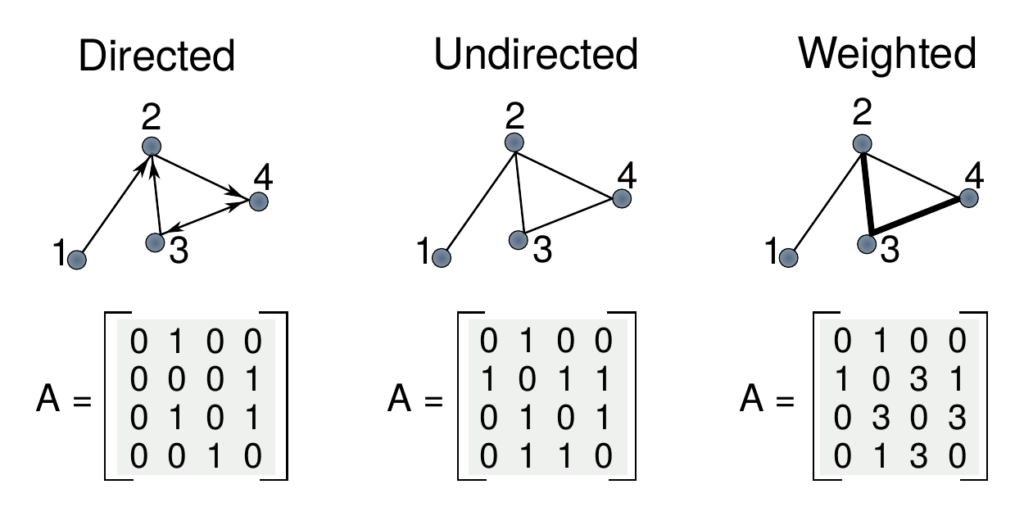
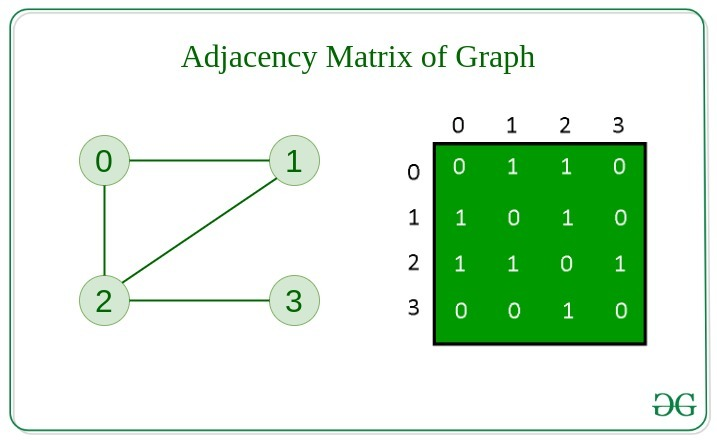
Adjacency Matrix
인접 행렬은 그래프에서 노드 간의 연결을 나타내는 데 사용되는 정사각형 행렬입니다.
행렬의 각 셀은 해당 노드 사이에 연결이 있는지 여부를 나타내며,
값 1은 가장자리를 나타내고 0은 연결이 없음을 나타냅니다.
이 행렬은 특히 간선이 많은 조밀한 그래프의 경우 그래프 구조를 저장하고 분석하는 간단한 방법을 제공합니다.
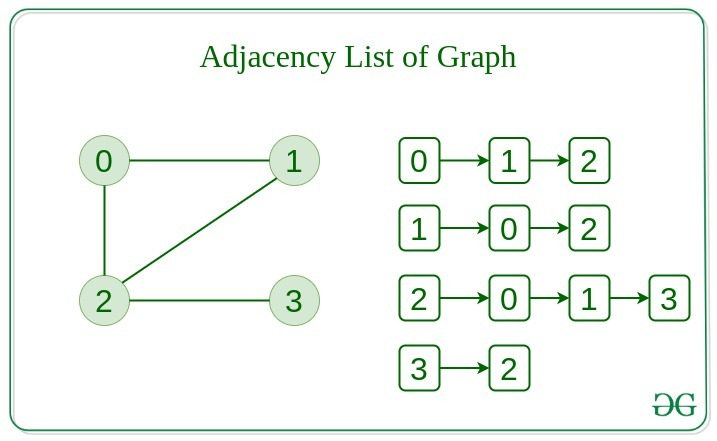
Adjacency List
이 그래프는 연결된 리스트의 모음으로 표시됩니다. 해당 노드에 연결된 간선을 가리키는 포인터 배열이 있습니다.
리스트 형태와 매트릭스 형태 무엇이 좋을까?
그래프를 매트릭스로 저장했을 때와 리스트로 저장했을 때의 시간복잡도는 아래와 같습니다
| Action | Adjacency Matrix | Adjacency List |
|---|---|---|
| Adding Edge | O(1) | O(1) |
| Removing an edge | O(1) | O(N) |
| Initializing | O(N*N) | O(N) |
그래프에 많은 수의 간선이 포함된 경우 행렬의 일부 항목만 비어 있으므로 그래프를 행렬로 저장하는 것이 좋습니다.
반대로 간선이 거의 없는 드문 드문한 그래프는 리스트 방식을 사용하는 게 좋습니다.
| 시나리오 | 더 나은 표현 |
|---|---|
| 간선이 거의 없는 그래프 | List |
| 노드가 많은 조밀한 그래프 | Matrix |
| 메모리 효율성 | List |
| 구현 용이성 | List |
| edge 제거 용이성 | Matrix |
그래프 구조를 이용한 애플리케이션
수많은 현실 세계의 수많은 응용 프로그램이 그래프로 이루어져 있습니다
소셜 네트워크
Facebook이나 LinkedIn과 같은 소셜 네트워크에서 노드는 사용자를 나타내고 가장자리는 사용자 간의 우정이나 연결을 나타냅니다.
네트워크 라우팅
컴퓨터 네트워크에서 노드는 라우터를 나타내고 에지는 라우터 간의 연결을 나타냅니다. 그래프 알고리즘은 데이터가 한 노드에서 다른 노드로 이동하는 최단 경로를 찾는 데 도움이 됩니다.
웹 페이지 연결
웹에서 노드는 웹 페이지를 나타내고 가장자리는 페이지 간의 하이퍼링크를 나타냅니다. Google과 같은 검색 엔진은 그래프 알고리즘을 사용하여 웹 페이지의 관련성과 인기를 결정합니다.
그래프 구조 장점과 단점
장점
그래프는 다양한 관계와 데이터 구조를 표현하는 데 유연한 데이터 구조입니다.
경로 찾기, 데이터 클러스터링, 네트워크 분석 및 기계 학습과 같은 다양한 문제를 모델링하고 해결하는 데 사용할 수 있습니다.
그래프 알고리즘은 종종 매우 효율적이며 복잡한 문제를 신속하고 효과적으로 해결할 수 있습니다.
복잡한 데이터 구조를 간단하고 직관적인 방식으로 표현할 수 있어 이해하기 쉽고 분석하기 쉽습니다.
단점
그래프는 그래프 이론이나 관련 알고리즘에 익숙하지 않은 사람들에게는 복잡하고 이해하기 어려울 수 있습니다.
그래프를 생성하고 조작하는 것은 특히 매우 크거나 복잡한 그래프의 경우 계산 비용이 많이 들 수 있습니다.
그래프 알고리즘을 설계하고 구현하는 것은 어려울 수 있으며 버그와 오류에 취약할 수 있습니다.
매우 크거나 복잡한 그래프의 경우 시각화 및 분석이 어려울 수 있으며 데이터에서 의미 있는 통찰을 얻는 것이 어려울 수 있습니다.
참고하면 좋은 글
https://www.geeksforgeeks.org/introduction-to-graphs-data-structure-and-algorithm-tutorials/
