BFS 란?
BFS(Breadth First Search)는 그래프에서 발생하는 사건들을 검사 혹은 처리하기 위해 탐색하는 방법 중 하나 입니다.
BFS는 그래프를 수준별로 탐색하여 다음 수준으로 이동하기 전에 주어진 노드의 모든 인접 노드를 방문하는 그래프 순회 알고리즘입니다.
BFS vs DFS
BFS와 같은 탐색 알고리즘에서 가장 먼저 비교되는 게 DFS인데요
BFS는 레벨별로 그래프를 탐색하여 다음 레벨로 이동하기 전에 주어진 노드의 모든 인접 정점을 방문하는 반면, DFS(Depth First Search)는 역추적하기 전에 각 분기를 따라 가능한 한 멀리 탐색합니다.
아래 그림을 통해 BFS와 DFS가 탐색을 어떻게 다르게 하는지 확인해보세요.
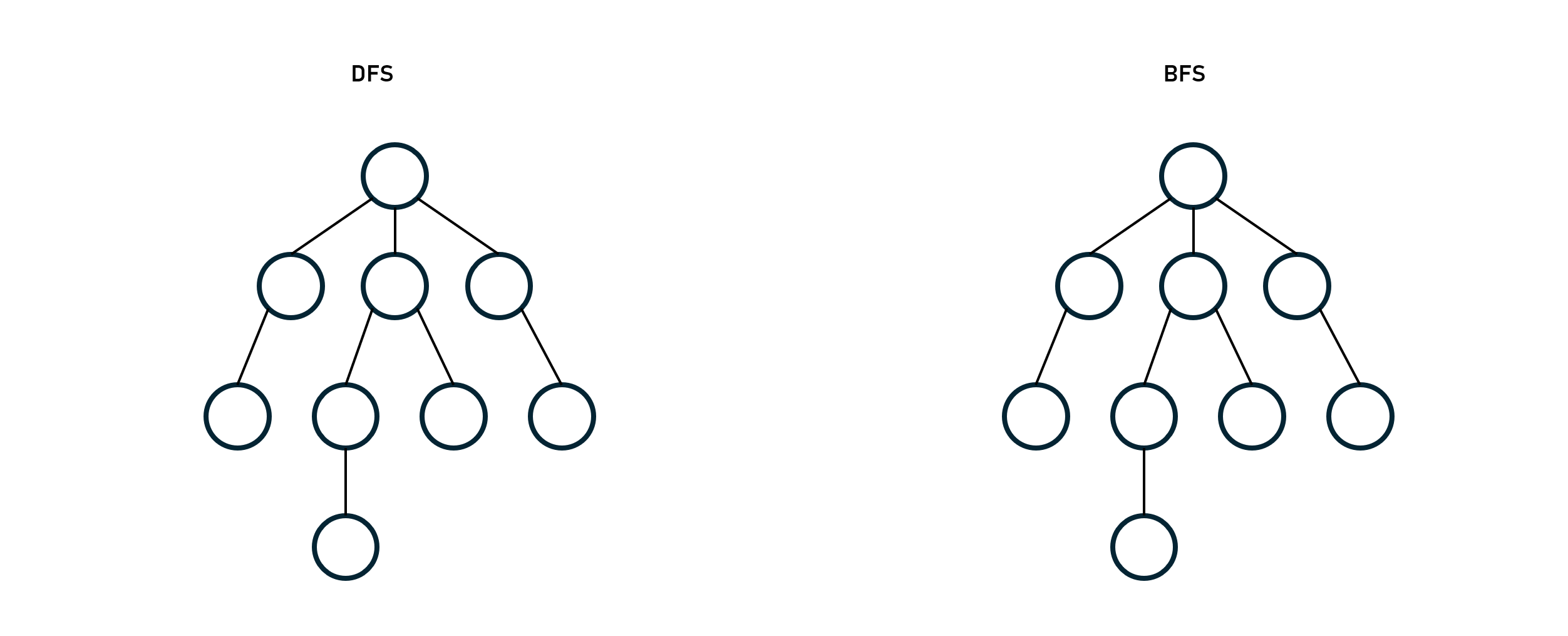
탐색 방법을 보시면 BFS는 시작점에 가장 가까운 노드 방문을 우선시하므로 최단 경로를 찾는 데 적합하다는 걸 알 수 있습니다.
반면 DFS는 메모리 효율성이 뛰어나 주기 감지와 같은 작업에 자주 사용된다고 합니다.
그래프 구현
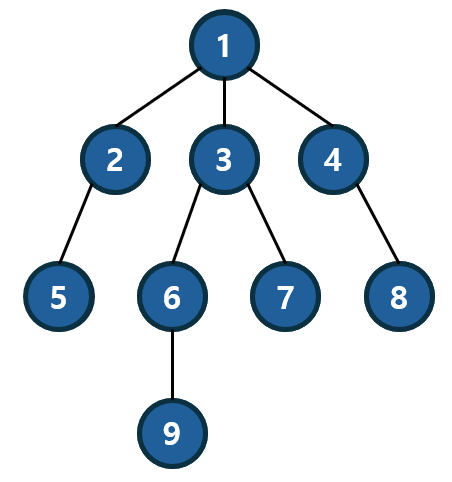
BFS와 같은 탐색 알고리즘을 수행하기 전에 우선 탐색을 할 그래프 구조를 만들어야 합니다.
트리 그래프는 원형인 “노드 (node)”와 이를 이어주는 “간선 (혹은 edge)”으로 구성된 것을 알 수 있습니다.
(그래프에 대해 궁금하시면 아래 글을 참고하세요)
하지만 데이터 타입 중에 트리라는 데이터 타입은 없습니다.
대신에 트리 구조를 배열, 딕셔너리와 같은 데이터 타입을 이용해서 아래와 같이 표현 할 수 있습니다.
그래프를 딕셔너리로 구현

tree = {
1:[2,3,4],
2:[1,5],
3:[1,6,7],
4:[1,7],
5:[2],
6:[3,9],
7:[3],
8:[4],
9:[6],
}그래프를 리스트 혹은 배열로 구현

연산 중에 인덱스 0은 직관적이지 않기 때문에 0번째 인덱스는 0으로 채우고, 1번째 인덱스가 1을 나타나게 하였습니다.
tree = [
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 1, 1, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 1],
[0, 0 ,0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
]tree = [
[0],
[2, 3, 4],
[1, 5],
[1, 6, 7],
[1, 8],
[2],
[3, 9],
[3],
[4],
[6],
]파이썬으로 BFS 구현
저는 트리 구조를 리스트로 표현해서 BFS를 작성해보았는데요
deque로 상위 노드부터 차례로 탐색하는 과정을 아래와 같이 구현할 수 있습니다.

from collections import deque
# 트리구조
trees = [
[0],
[2, 3, 4],
[1, 5],
[1, 6, 7],
[1, 8],
[2],
[3, 9],
[3],
[4],
[6],
]
# 하단의 코드들은 모두 BFS를 위한 코드
queue = deque([1])
visited_nodes = []
def action_for_node(node):
# 해당 노드를 방문했음을 체크하기
visited_nodes.append(node)
def search_node(node):
linked_nodes = trees[node]
for linked_node in linked_nodes:
if linked_node in visited_nodes:
linked_nodes.remove(linked_node)
return linked_nodes
while queue: # 큐에 노드가 남아있다면
print(queue) # BFS인지 출력
node = queue.popleft() # 큐에서 왼쪽 노드 뽑기
action_for_node(node) # 노드에 대한 처리, 방문지 처리
next_nodes = search_node(node) # 다음 노드 찾기
for next_node in next_nodes:
queue.append(next_node) # 연결된 노드를 넣어줌
# print()
# deque([1])
# deque([2, 3, 4])
# deque([3, 4, 5])
# deque([4, 5, 6, 7])
# deque([5, 6, 7, 8])
# deque([6, 7, 8])
# deque([7, 8, 9])
# deque([8, 9])
# deque([9])BFS 장점
비가중 그래프에서 최단 경로 보장
가중치가 없는 그래프에 한해서 최단 경로 찾기가 가능합니다.
BFS는 다음 레벨로 이동하기 전에 동일한 거리 레벨에서 모든 인접 노드를 탐색하여 이동하기 때문에 DFS와 달리 제일 먼저 얻어진 해가 최단 경로가 된다는 보장을 가집니다.
완전성
BFS는 솔루션이 존재하는 경우 결국 솔루션을 찾도록 보장합니다.
초기 노드부터 가능한 모든 경로를 체계적으로 탐색하여 돌이킬 수 없는 일이 없도록 보장합니다.
따라서 그래프 기반 문제에서 솔루션을 찾는 데 신뢰할 수 있는 알고리즘이 됩니다.
무한에 가까운 depth를 가진 그래프도 탐색이 가능하다
depth는 너무 깊은 데, 근처 노드만 탐색하고 싶을 때는 BFS를 사용하는 게 좋을 수 있습니다.
직관성
DFS 구현 보다는 직관적으로 이해하기 쉽습니다.
BFS 단점
메모리 소비
BFS의 주요 단점 중 하나는 특히 큰 그래프의 경우 메모리 소비가 높다는 것입니다.
BFS는 방문해야 하는 노드를 저장하기 위해 대기열을 유지 관리하며, 이 대기열은 크기가 크게 증가하여 많은 메모리를 소비할 수 있습니다.
매우 큰 그래프의 경우 또는 메모리 리소스가 제한된 경우 BFS가 실행 가능하지 않을 수 있습니다.
밀도 그래프에는 비효율적
BFS는 다음 레벨로 이동하기 전에 노드의 모든 이웃을 탐색합니다.
대부분의 노드가 서로 연결된 조밀한 그래프에서는 BFS가 각 수준에서 많은 수의 노드를 탐색하게 되어 비효율성을 초래할 수 있습니다.
이로 인해 실행 시간이 길어지고 성능이 저하될 수 있습니다.
가중치 그래프에 적합하지 않음
BFS는 간선의 가중치나 비용이 다른 가중치 그래프에서 최단 경로를 찾는 데 적합하지 않습니다.
BFS는 모든 가장자리를 동일하게 처리하고 노드 수준을 수준별로 탐색하므로 가중치 그래프에서 항상 최단 경로를 찾지 못할 수도 있습니다.
이러한 경우에는 Dijkstra 또는 A*와 같은 알고리즘이 더 적합합니다.
무한 그래프를 처리하지 않습니다
BFS는 무한 그래프나 주기가 있는 그래프를 처리하도록 설계되지 않았습니다.
그래프에 사이클이나 무한 경로가 포함된 경우 BFS는 무한 루프에 걸려 종료할 수 없습니다.
이러한 제한으로 인해 BFS는 동적 네트워크나 무한 그리드를 나타내는 그래프와 같은 특정 유형의 그래프에 적합하지 않습니다.
참고하면 좋은 글