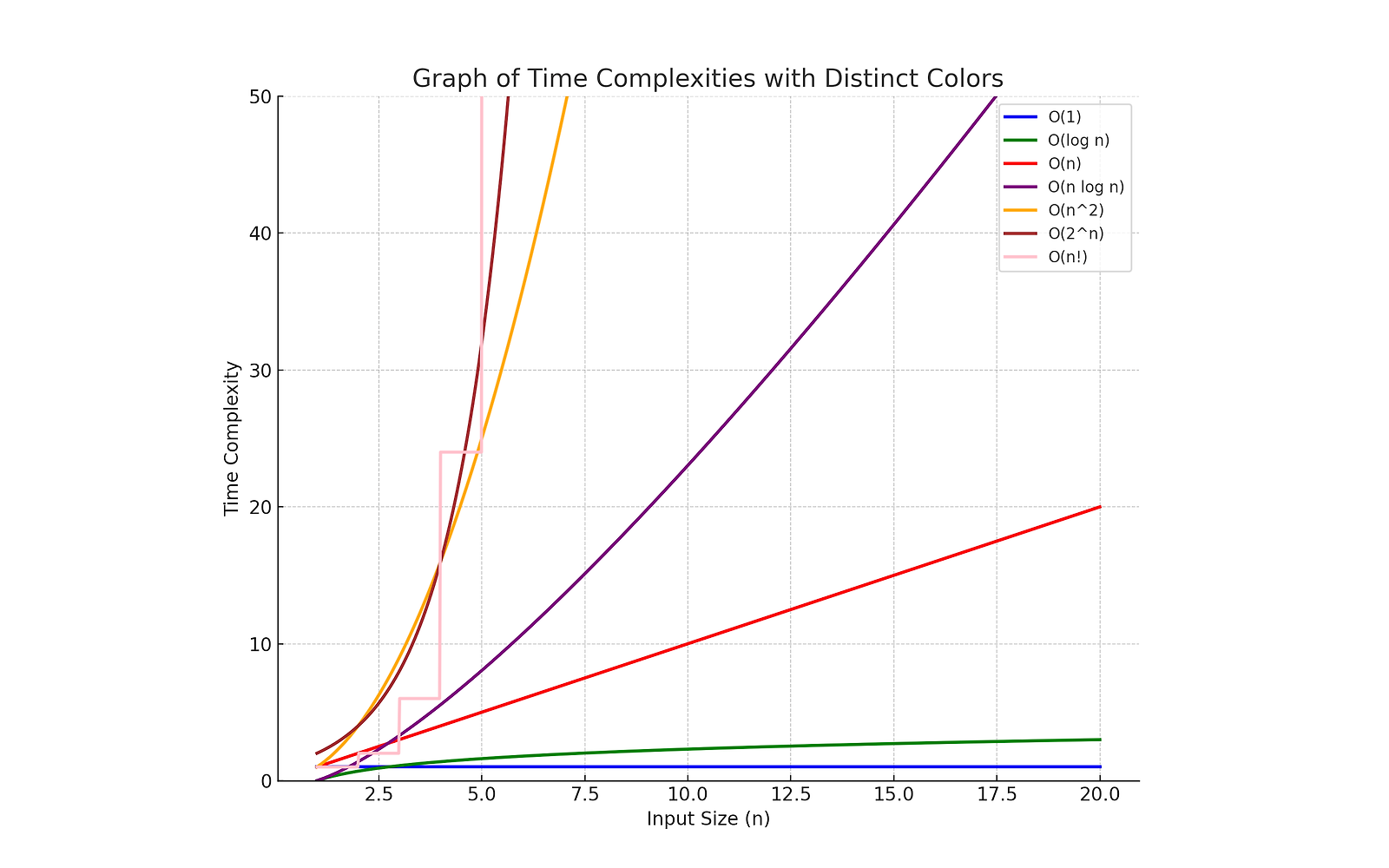
시간 복잡도와 공간 복잡도에 대한 공부한 내용을 정리해 보았습니다.
- 시간 복잡도 (Time Complexity) : 실행에 필요한 시간을 평가한 것
- 공간 복잡도 (Space Complexity) : 메모리 영역과 파일 공간이 얼마나 필요한가를 평가한 것
시간 복잡도
시간 복잡도는 입력 크기가 증가함에 따라 알고리즘의 실행 시간이 어떻게 증가하는지를 측정한 것입니다.
Big-O 표기법은 최악의 시나리오에서 알고리즘의 시간 복잡도의 상한을 표현하는 방법입니다.
이는 특정 하드웨어, 상수 요소 또는 하위 항의 세부 사항에 얽매이지 않고 알고리즘의 효율성을 분석하는 데 도움이 됩니다.
Big-O는 다음과 같이 계산 합니다.
- 기본 연산 계산: 알고리즘에서 수행되는 기본 작업을 식별하는 것부터 시작하세요. 이는 산술 연산, 할당 또는 비교일 수 있습니다.
- 입력 크기 결정: 알고리즘의 실행 시간이 입력 크기에 따라 어떻게 달라지는지 이해합니다. 입력 크기는 일반적으로 ‘n’으로 표시됩니다.
- 시간 복잡도 표현: Big-O 표기법을 사용하여 최악의 시간 복잡도를 표현합니다. 일반적인 표기법에는 상수 시간의 경우 O(1), 로그 시간의 경우 O(log n), 선형 시간의 경우 O(n), 2차 시간의 경우 O(n^2) 등이 포함됩니다.
시간 복잡도는 다음과 같이 요약 정리할 수 있습니다.
| 시간 복잡도 | Big-O | 특징 | 예제 알고리즘 |
|---|---|---|---|
| 상수 | O(1) | – 실행 시간은 입력 크기에 관계없이 일정하게 유지됩니다. | 인덱스를 사용하여 배열의 요소에 액세스 |
| 로그 | O(log n) | – 각 작업마다 입력 크기를 나눕니다. | 정렬된 리스트의 이진 검색 |
| 선형 | O(n) | – 실행 시간은 입력 크기에 따라 선형적으로 늘어납니다. | 리스트의 요소를 반복 |
| 선형 로그 | O(n log n) | – 문제를 분할하고 각 부분에 로그 연산을 적용하는 알고리즘에서 흔히 사용됩니다. | 병합 정렬, 힙 정렬, 퀵 정렬. |
| 2차 | O(n^2) | – 실행 시간은 입력 크기의 제곱에 비례합니다. | 2D 배열의 요소를 반복하는 중첩 루프 |
| 지수 | O(2^n) | – 입력 크기가 추가될 때마다 실행 시간이 두 배로 늘어납니다. | 피보나치 수열과 같은 재귀 알고리즘 |
상수 복잡도 : O(1)
입력 크기에 관계없이 항상 일정한 실행 시간을 갖는 알고리즘을 의미합니다.
상수 연산
a = 5
b = 7
print(a + b)로그 복잡도 : O(log n)
입력 크기에 따라 실행 시간이 로그로 증가하는 알고리즘을 의미합니다.
이진 탐색 (Binary Search)은 정렬된 배열에서 특정 값을 찾는 알고리즘입니다.
입력 크기 N에 대해 이진 탐색은 최대 log₂(N) 단계만큼 수행됩니다.
아래는 이진 탐색의 예제 코드입니다
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
my_array = [1, 3, 5, 7, 9, 11, 13]
target_value = 7
result_index = binary_search(my_array, target_value)
if result_index != -1:
print(f"Found at index {result_index}")
else:
print("Not found")선형 복잡도 : O(n)
입력 크기에 비례하여 실행 시간이 선형적으로 증가하는 알고리즘을 의미합니다.
예를 들어, 입력 데이터의 크기가 두 배로 증가하면 실행 시간도 비례하여 증가하는 복잡도 입니다.
리스트의 모든 요소를 한 번씩 순회하는 경우 O(n) 시간이 소요됩니다. 아래는 리스트의 모든 요소를 출력하는 예제 코드입니다
def print_list_elements(my_list):
for item in my_list:
print(item)
my_list = [1, 2, 3, 4, 5]
print_list_elements(my_list)선형 로그 복잡도 : O(n log n)
입력 크기에 비례하여 실행 시간이 선형로그(log-linear)적으로 증가하는 알고리즘을 의미합니다.
배열의 모든 요소에 대해서 로그 스케일의 연산을 수행하는 예를 확인해주세요.
def print_pairs_log_times(arr):
for element in arr:
j = len(arr)
while j > 0:
print(f"({element}, {j})")
# // 정수 몫 연산자
j //= 2
# 예시: 각 요소에 대해 로그 스케일로 반복 (O(nlogn))
print_pairs_log_times([1, 2, 3])모든 요소 (n)을 돌면서 while 문으로 log n 만큼 연산 하는 것을 확인 할 수 있습니다.
2차 복잡도 : O(n²)
데이터양이 증가할수록 데이터양의 제곱만큼 연산량 증가하는 알고리즘 입니다. 이중 for문이 대표적인 2차 복잡도 알고리즘 입니다.
for i in range(n):
sum_ = 0
for j in range(n):
# 2n + n
sum_ += i O(2^n) 지수 복잡도
지수 복잡도는 매 단계마다 연산의 수가 두 배씩 증가합니다.
간단한 예로는 피보나치 수열의 재귀적 계산이 있습니다.
재귀를 하면서 연산이 2배씩 계속 증가하기 때문에 2^n의 복잡도를 가지는 것을 확인 할 수 있습니다.
pythonCopy code
def fibonacci_simple(n):
if n <= 1:
return n
return fibonacci_simple(n-1) + fibonacci_simple(n-2)
# 피보나치 수열 계산
print(fibonacci_simple(5)) # 출력: 5 (0, 1, 1, 2, 3, 5)알고리즘 문제 풀 시, 시간 복잡도 제한
시간 제한 1초 인 경우, 다음과 같은 시간 복잡도 내에서 풀어야 합니다.
- N의 범위가 500 경우 O(N^3)
- N의 범위가 2,000 경우 O(N^2)
- N의 범위가 100,000 O(n log n)
- N의 범위가 10,000,000 O(N)
공간 복잡도
공간 복잡도는 입력 크기가 증가함에 따라 알고리즘의 메모리 사용량이 어떻게 증가하는지 측정합니다.
고정 공간, 가변 공간
메모리 양을 계산하기에 앞서 2가지 개념에 대해서 알아야 합니다. 고정 공간, 가변 공간
고정 공간(Fixed space)는 입력 크기에 관계없이 알고리즘이 실행될 때 항상 일정한 메모리 양을 사용하는 경우를 의미합니다.
반면에 가변 공간(variable space)는 입력 크기에 따라 알고리즘이 사용하는 메모리 양이 변하는 경우를 의미합니다.
고정 공간은 상수이므로 공간 복잡도는 가변 공간에 좌우됩니다.
일정한 공간 복잡도 : O(1)
일정한 공간 복잡도는 사용되는 공간이 입력 크기(O(1))에 의존하지 않는다는 것을 의미합니다.
def constant_space_example(arr):
total = 0
for item in arr:
total += item
return total위의 예제에서 ‘total’이 사용하는 공간은 배열 크기에 관계없이 일정하게 유지됩니다.
선형 공간 복잡도 : O(n)
선형 공간 복잡도는 입력 크기(O(n))에 따른 공간의 선형 증가를 나타냅니다.
def linear_space_example(n):
arr = [0] * n
return arr2차 공간 복잡도(O(n^2))
2차 공간 복잡도는 공간의 2차 증가(O(n^2))를 의미합니다.
2차 리스트가 있고 그 크기가 입력 크기에 비례해서 증가한다면 2차 공간 복잡도를 가지게 됩니다.
def quadratic_space_example(n):
arr_2d = [[0] * n for _ in range(n)]
return arr_2d시간 복잡도 vs 공간 복잡도
시간 복잡도와 공간 복잡도 사이의 관계를 이해하는 것은 효율적인 알고리즘을 만드는 데 중요합니다.
Trade off
시간복잡도와 공간복잡도 사이에는 상충관계가 존재하는 경우가 있습니다. 하나를 향상시키면 다른 하나가 희생될 수 있습니다.
메모리 사용량
공간 복잡도는 메모리 사용량에 초점을 맞추는 반면, 시간 복잡도는 실행 시간과 관련이 있습니다. 그들은 알고리즘의 효율성을 평가할 때 서로를 보완합니다.
시간 복잡도 또는 공간 복잡도 우선순위
많은 분들이 이제는 하드웨어 성능이 뛰어나졌기 때문에 공간 복잡도 보다는 시간 복잡도가 중요하다고 말씀해주셨습니다.
다만 공간 복잡도도 우선 순위가 높을 때도 있습니다.
바로 “메모리가 제한 환경“입니다.
임베디드 시스템이나 모바일 장치와 같이 메모리가 제한된 환경에서는 공간 복잡성에 중점을 두어야 한다고 합니다.